Allowable Stresses for FRP Pipe Stress Analysis

In our last article, we looked at how the elastic properties of a laminate are determined. In this article, we continue our look at the mechanical properties that are required to conduct a pipe stress analysis, this time at the strength properties, or to be more specific, the allowable stresses.

As we discussed in our article on Pressure Design of FRP Components, we need an allowable hoop stress to determine the component thickness required for any particular pressure capability. For pipe stress analysis, we are more concerned with allowable axial stresses. For isotropic materials such as steel, the allowable stresses are listed in the ASME Piping Codes, so if we were working with steel we could just select the appropriate value for the given design temperature.

ASME NM.2

It is not quite so simple with FRP piping, as allowable stresses have not been standardized to the same extent as metallic materials. However, it is possible to list appropriate values for a few standard constructions, and that is what has been done in the new ASME Standard for FRP Piping (ASME NM.2). That Standard (via its companion standard NM.3) provides both elastic properties and allowable stress values for three types of construction: Type I, Type II, and Type III laminates. Type I and II are contact molded laminates as defined in ASTM C582. A Type III laminate is a 55 deg filament wound laminate as defined in NM.2. For other types of laminates, or for values that are more appropriate to a manufacturer’s constructions, it is necessary to consult with the manufacturer. It is not possible to rely on Mechanics of Composites for allowable stresses to the same extent as for elastic properties. The allowable stresses must be determined through testing of the specific laminate of interest, or by using conservative estimates based on previous testing of similar laminates.

The strength values must be reduced by appropriate design factors to arrive at suitable allowable stresses. ASME NM.2 provides minimum design factors that must be used, and these design factors are based on the type of testing that is used to determine the laminate strength, i.e. short term versus long term testing. For example, for laminate strengths based on short term testing, a minimum design factor of 6 is required for sustained loads.

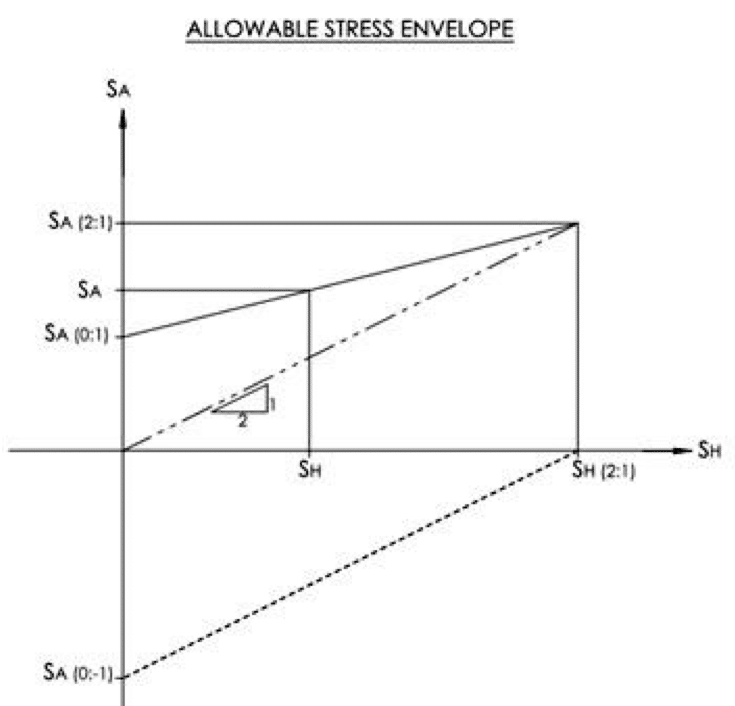
For “quasi-isotropic” laminates such as Type I and Type II laminates, it is usually sufficient to determine the allowable axial stress by conducting a uniaxial strength test of the laminate and dividing the strength by a suitable design factor such as 6. For orthotropic laminates such as Type III (55 deg filament wound laminate), the axial strength can depend on the magnitude of the coincident hoop stress. It is therefore necessary to determine the axial strength under at least two different loading conditions:

  1. Hoop stress that is twice that of the axial stress
  2. Hoop stress that is zero

During a pressure test, the hoop stress is twice that of the axial stress, so a pressure test is used to determine the axial strength under “biaxial” loading. A simple tensile test can be used to determine the uniaxial strength of the laminate. Two allowable stresses are determined by dividing the two axial strengths by suitable design factors. These allowable stresses are then used to create the “allowable stress envelope”, demonstrated here.

In the allowable stress envelope, the hoop stress is plotted along the X axis, and the axial stress is plotted along the Y axis. The allowable axial stress for the biaxial stress state is represented by SA(2:1) and the allowable axial stress for the case where the hoop stress is zero is represented by SA(0:1). A straight line is drawn between these two points to provide the allowable stress at any intermediate hoop stress, i.e. at pressures lower than the maximum allowable design pressure. The distance between the allowable stress line and the 2:1 stress line (shown as a dashed line in the figure) represents the allowable axial stress that is available for loads other than pressure.

It should be noted that if the applied hoop stress is equal to the maximum allowable hoop stress, then there is no distance between the allowable stress line and the 2:1 stress line, and there would be no allowable stress available for axial loads other than pressure. This goes back to our earlier discussion on pressure design of filament wound pipe, and why we said it was necessary to provide additional capacity in some laminates. For example, for design of filament wound pipe, RPS uses a design factor of 10 when applied to the short term hoop tensile strength, rather than the 6 that would be expected under combined loading. This higher design factor will result in a greater wall thickness than that required just for pressure containment and will provide a significant additional axial load-carrying capacity for the non-pressure axial loads.

One further point to note about the allowable stress envelope: When the axial stress is compressive rather than tensile, as would typically be the case for rigidly restrained systems, the allowable stress is based on the axial compressive strength, i.e SA(0:-1). It is acceptable to simply use the negative of the axial tensile strength (SA(0:1)) for this value as the compressive strength is greater than the tensile strength, but it is typically worth testing to determine this value as the compressive strength can be much greater than the tensile strength.

In our next article we’ll take a look at stress intensification factors (SIFs) and flexibility factors (k’s).

Previous article in the series: Elastic Properties for Pipe Stress Analysis

Next in the series: Stress Intensification and Flexibility Factors