In our previous article, we took our first look at pressure design of piping components by looking at pipe. We are going to continue that discussion by looking at pressure design of FRP pipe fittings and joints.
As we noted in our last article, pipe is by far the simplest component to design in any piping system. The stresses in a pipe when exposed to pressure are:
\[S_h=\frac{P \cdot I D_s}{2 \cdot T_s} \quad\text { and }\quad S_{a x}=\frac{P \cdot I D_s}{4 \cdot T_s}
\]
where:
Sh = Hoop stress
Sax = Axial stress
P = Pressure
IDs = Inside diameter of structural wall
Ts = Thickness of structural wall
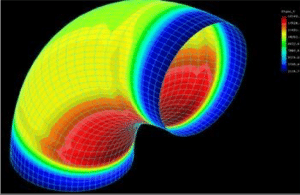
The situation isn’t quite so simple for most fittings. The geometry of fittings gives rise to local stresses within the fitting that can be significantly greater than those calculated using the equations above. The most common method for dealing with these higher stresses is to include a “fudge factor” with one or both of the above equations. This fudge factor is called the pressure stress multiplier. It is usually designated by the letter “m”, and it represents the ratio of the maximum pressure stress in the fitting to the pressure stress in an equivalent pipe.
The equation for hoop stress would then become:
\[S_h=\frac{m \cdot P \cdot I D_s}{2 \cdot T_s}
\]
For example, in a long radius elbow of uniform thickness, the maximum hoop stress in the elbow is 1.25 times that in a pipe, so m = 1.25. This means that a long radius elbow should be at least 1.25 times as thick as a pipe to provide the same factor of safety against burst. (This statement is only true if the pipe and elbow are manufactured using the same type of laminate; a situation that is most often not the case. The elbow could be thinner or thicker than the 1.25 times depending on the relative strengths of the elbow and pipe laminates).