It is not quite so simple with FRP piping, as allowable stresses have not been standardized to the same extent as metallic materials. However, it is possible to list appropriate values for a few standard constructions, and that is what has been done in the new ASME Standard for FRP Piping (ASME NM.2). That Standard (via its companion standard NM.3) provides both elastic properties and allowable stress values for three types of construction: Type I, Type II, and Type III laminates. Type I and II are contact molded laminates as defined in ASTM C582. A Type III laminate is a 55 deg filament wound laminate as defined in NM.2. For other types of laminates, or for values that are more appropriate to a manufacturer’s constructions, it is necessary to consult with the manufacturer. It is not possible to rely on Mechanics of Composites for allowable stresses to the same extent as for elastic properties. The allowable stresses must be determined through testing of the specific laminate of interest, or by using conservative estimates based on previous testing of similar laminates.
The strength values must be reduced by appropriate design factors to arrive at suitable allowable stresses. ASME NM.2 provides minimum design factors that must be used, and these design factors are based on the type of testing that is used to determine the laminate strength, i.e. short term versus long term testing. For example, for laminate strengths based on short term testing, a minimum design factor of 6 is required for sustained loads.
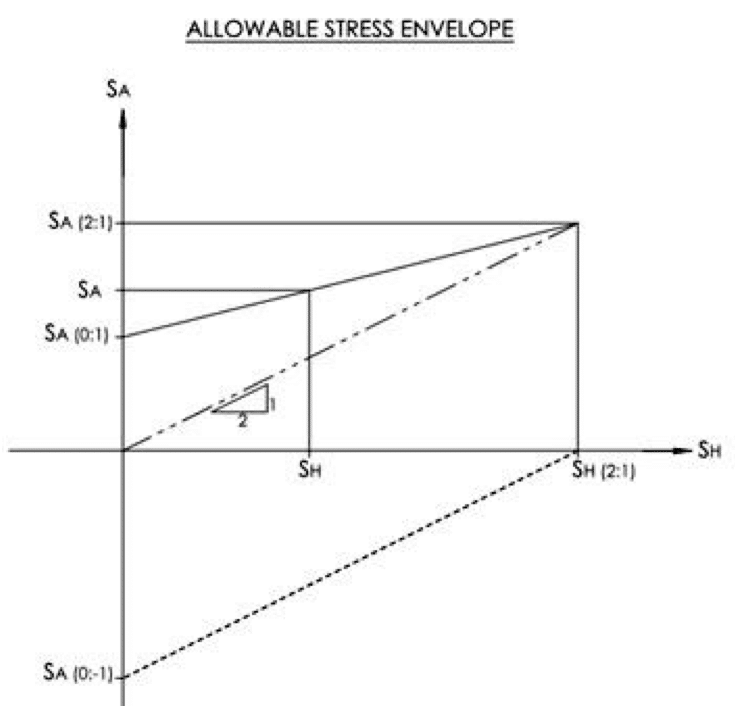
For “quasi-isotropic” laminates such as Type I and Type II laminates, it is usually sufficient to determine the allowable axial stress by conducting a uniaxial strength test of the laminate and dividing the strength by a suitable design factor such as 6. For orthotropic laminates such as Type III (55 deg filament wound laminate), the axial strength can depend on the magnitude of the coincident hoop stress. It is therefore necessary to determine the axial strength under at least two different loading conditions:
- Hoop stress that is twice that of the axial stress
- Hoop stress that is zero
During a pressure test, the hoop stress is twice that of the axial stress, so a pressure test is used to determine the axial strength under “biaxial” loading. A simple tensile test can be used to determine the uniaxial strength of the laminate. Two allowable stresses are determined by dividing the two axial strengths by suitable design factors. These allowable stresses are then used to create the “allowable stress envelope”, demonstrated here.